
Basis Sets
Basis sets in PSI4 are Gaussian functions (not Slater-type functions or plane waves),
all-electron [no effective core potentials (ECPs)],
and of Gaussian94 format (for ease of export from EMSL).
Both spherical harmonic (5D/7F) and Cartesian (6D/10F) Gaussian functions are supported,
but their mixtures are not, neither within a basis set (e.g., 6D/7F) nor within a calculation
(e.g., cartesian for the orbital basis and spherical for the fitting basis).
For built-in basis sets, the correct spherical/cartesian value for PUREAM
is set internally from the orbital basis.
Tables Pople,
Dunning,
Dunning (Douglas-Kroll), and
Other summarize the orbital basis sets available in
PSI4. These tables are arranged so that columns indicate degree of
augmentation by diffuse functions (generally necessary for anions, excited
states, and noncovalent interactions) and DTQ56 indicate the 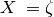 levels
available. Several intermediate levels of diffuse space between the customary
non-augmented and augmented versions have been supplied for each basis set,
including heavy-augmented and Truhlar’s [Papajak:2011:10] calendar
truncations described in Table Months Bases. Fitting bases
in Tables JKFIT,
RI, and DUAL
are available for methods incorporating density-fitting or dual-basis
approximations. JKFIT sets are appropriate for fitting
levels
available. Several intermediate levels of diffuse space between the customary
non-augmented and augmented versions have been supplied for each basis set,
including heavy-augmented and Truhlar’s [Papajak:2011:10] calendar
truncations described in Table Months Bases. Fitting bases
in Tables JKFIT,
RI, and DUAL
are available for methods incorporating density-fitting or dual-basis
approximations. JKFIT sets are appropriate for fitting 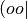 -type products,
such as encountered in SCF theory and the electrostatics/exchange terms of SAPT.
RI sets are appropriate for fitting
-type products,
such as encountered in SCF theory and the electrostatics/exchange terms of SAPT.
RI sets are appropriate for fitting 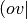 -type products, such as encountered in
MP2 and most SAPT terms. Citations for basis sets can be found in their
definition files at psi4/lib/basis in the source. For basis set availability by
element and the default value for keyword PUREAM, consult
Appendix Basis Sets by Element.
-type products, such as encountered in
MP2 and most SAPT terms. Citations for basis sets can be found in their
definition files at psi4/lib/basis in the source. For basis set availability by
element and the default value for keyword PUREAM, consult
Appendix Basis Sets by Element.
Summary of Pople-style orbital basis sets available in PSI4
| no diffuse |
heavy-augmented |
augmented |
|---|
| basis set |
[alias] |
basis set |
[alias] |
basis set |
[alias] |
|---|
| STO-3G |
|
|
|
|
|
| 3-21G |
|
|
|
|
|
| |
|
|
|
|
|
| 6-31G |
|
6-31+G |
|
6-31++G |
|
| 6-31G(d) |
[6-31G*] |
6-31+G(d) |
[6-31+G*] |
6-31++G(d) |
[6-31++G*] |
| 6-31G(d_p) |
[6-31G**] |
6-31+G(d_p) |
[6-31+G**] |
6-31++G(d_p) |
[6-31++G**] |
| |
|
|
|
|
|
| 6-311G |
|
6-311+G |
|
6-311++G |
|
| 6-311G(d) |
[6-311G*] |
6-311+G(d) |
[6-311+G*] |
6-311++G(d) |
[6-311++G*] |
| 6-311G(d_p) |
[6-311G**] |
6-311+G(d_p) |
[6-311+G**] |
6-311++G(d_p) |
[6-311++G**] |
| 6-311G(2d) |
|
6-311+G(2d) |
|
6-311++G(2d) |
|
| 6-311G(2d_p) |
|
6-311+G(2d_p) |
|
6-311++G(2d_p) |
|
| 6-311G(2d_2p) |
|
6-311+G(2d_2p) |
|
6-311++G(2d_2p) |
|
| 6-311G(2df) |
|
6-311+G(2df) |
|
6-311++G(2df) |
|
| 6-311G(2df_p) |
|
6-311+G(2df_p) |
|
6-311++G(2df_p) |
|
| 6-311G(2df_2p) |
|
6-311+G(2df_2p) |
|
6-311++G(2df_2p) |
|
| 6-311G(2df_2pd) |
|
6-311+G(2df_2pd) |
|
6-311++G(2df_2pd) |
|
| 6-311G(3df) |
|
6-311+G(3df) |
|
6-311++G(3df) |
|
| 6-311G(3df_p) |
|
6-311+G(3df_p) |
|
6-311++G(3df_p) |
|
| 6-311G(3df_2p) |
|
6-311+G(3df_2p) |
|
6-311++G(3df_2p) |
|
| 6-311G(3df_2pd) |
|
6-311+G(3df_2pd) |
|
6-311++G(3df_2pd) |
|
| 6-311G(3df_3pd) |
|
6-311+G(3df_3pd) |
|
6-311++G(3df_3pd) |
|
Levels of truncation for diffuse functions in standard basis sets
| augmentation level |
angular momenta in the diffuse space |
valid basis sets |
|---|
| |
Li-Kr main group |
H & He |
D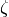 |
T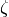 |
Q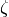 |
|---|
| aug-cc-pVXZ |
s, p, 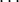 , , 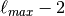 , , 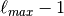 , , 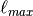 |
s, p, 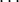 , , 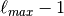 |
aDZ |
aTZ |
aQZ |
| heavy-aug-cc-pVXZ |
s, p, 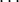 , , 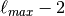 , , 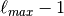 , , 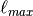 |
|
haDZ |
haTZ |
haQZ |
| jun-cc-pVXZ |
s, p, 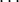 , , 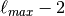 , , 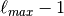 |
|
jaDZ |
jaTZ |
jaQZ |
| may-cc-pVXZ |
s, p, 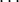 , , 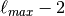 |
|
|
maTZ |
maQZ |
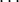 |
s, p |
|
|
|
aaQZ |
| cc-pVXZ |
|
|
DZ |
TZ |
QZ |
Summary of Dunning orbital basis sets available in PSI4
| basis set |
no diffuse |
feb |
mar |
apr |
may |
jun |
heavy-aug |
aug |
d-aug |
|---|
| cc-pVXZ |
DTQ56 |
6 |
56 |
Q56 |
TQ56 |
DTQ56 |
DTQ56 |
DTQ56 |
DTQ56 |
| cc-pV(X+d)Z |
DTQ56 |
6 |
56 |
Q56 |
TQ56 |
DTQ56 |
DTQ56 |
DTQ56 |
DTQ56 |
| cc-pCVXZ |
DTQ56 |
6 |
56 |
Q56 |
TQ56 |
DTQ56 |
DTQ56 |
DTQ56 |
DTQ56 |
| cc-pCV(X+d)Z |
DTQ56 |
6 |
56 |
Q56 |
TQ56 |
DTQ56 |
DTQ56 |
DTQ56 |
DTQ56 |
| cc-pwCVXZ |
DTQ5 |
|
5 |
Q5 |
TQ5 |
DTQ5 |
DTQ5 |
DTQ5 |
DTQ5 |
| cc-pwCV(X+d)Z |
DTQ5 |
|
5 |
Q5 |
TQ5 |
DTQ5 |
DTQ5 |
DTQ5 |
DTQ5 |
Summary of Dunning Douglas-Kroll orbital basis sets available in PSI4
| basis set |
no diffuse |
feb |
mar |
apr |
may |
jun |
heavy-aug |
aug |
d-aug |
|---|
| cc-pVXZ-DK |
DTQ5 |
|
|
|
|
|
DTQ5 |
DTQ5 |
|
| cc-pV(X+d)Z-DK |
|
|
|
|
|
|
|
|
|
| cc-pCVXZ-DK |
DTQ5 |
|
|
|
|
|
DTQ5 |
DTQ5 |
|
| cc-pCV(X+d)Z-DK |
|
|
|
|
|
|
|
|
|
| cc-pwCVXZ-DK |
–TQ5 |
|
|
|
|
|
–TQ5 |
–TQ5 |
|
| cc-pwCV(X+d)Z-DK |
|
|
|
|
|
|
|
|
|
Summary of Dunning JK-fitting basis sets available in PSI4
| basis set |
no diffuse |
feb |
mar |
apr |
may |
jun |
heavy-aug |
aug |
d-aug |
|---|
| cc-pVXZ-JKFIT |
DTQ5 |
|
5 |
Q5 |
TQ5 |
DTQ5 |
DTQ5 |
DTQ5 |
|
| cc-pV(X+d)Z-JKFIT |
DTQ5 |
|
5 |
Q5 |
TQ5 |
DTQ5 |
DTQ5 |
DTQ5 |
|
| cc-pCVXZ-JKFIT |
|
|
|
|
|
|
|
|
|
| cc-pCV(X+d)Z-JKFIT |
|
|
|
|
|
|
|
|
|
| cc-pwCVXZ-JKFIT |
|
|
|
|
|
|
|
|
|
| cc-pwCV(X+d)Z-JKFIT |
|
|
|
|
|
|
|
|
|
Summary of Dunning MP2-fitting basis sets available in PSI4
| basis set |
no diffuse |
feb |
mar |
apr |
may |
jun |
heavy-aug |
aug |
d-aug |
|---|
| cc-pVXZ-RI |
DTQ56 |
6 |
56 |
Q56 |
TQ56 |
DTQ56 |
DTQ56 |
DTQ56 |
|
| cc-pV(X+d)Z-RI |
DTQ56 |
6 |
56 |
Q56 |
TQ56 |
DTQ56 |
DTQ56 |
DTQ56 |
|
| cc-pCVXZ-RI |
|
|
|
|
|
|
|
|
|
| cc-pCV(X+d)Z-RI |
|
|
|
|
|
|
|
|
|
| cc-pwCVXZ-RI |
DTQ5 |
|
5 |
Q5 |
TQ5 |
DTQ5 |
DTQ5 |
DTQ5 |
|
| cc-pwCV(X+d)Z-RI |
DTQ5 |
|
5 |
Q5 |
TQ5 |
DTQ5 |
DTQ5 |
DTQ5 |
|
Summary of Dunning dual-basis helper basis sets available in PSI4
| basis set |
no diffuse |
feb |
mar |
apr |
may |
jun |
heavy-aug |
aug |
d-aug |
|---|
| cc-pVXZ-DUAL |
TQ |
|
|
|
|
|
TQ |
DTQ |
|
| cc-pV(X+d)Z-DUAL |
|
|
|
|
|
|
|
|
|
| cc-pCVXZ-DUAL |
|
|
|
|
|
|
|
|
|
| cc-pCV(X+d)Z-DUAL |
|
|
|
|
|
|
|
|
|
| cc-pwCVXZ-DUAL |
|
|
|
|
|
|
|
|
|
| cc-pwCV(X+d)Z-DUAL |
|
|
|
|
|
|
|
|
|
Summary of other orbital basis sets available in PSI4
| Karlsruhe |
other |
|---|
| no diffuse |
augmented |
|
|---|
| def2-SV(P) |
|
DZP |
| def2-SVP |
def2-SVPD |
TZ2P |
| def2-TZVP |
def2-TZVPD |
TZ2PF |
| def2-TZVPP |
def2-TZVPPD |
Sadlej-LPol-ds |
| def2-QZVP |
def2-QZVPD |
Sadlej-LPol-dl |
| def2-QZVPP |
def2-QZVPPD |
Sadlej-LPol-fs |
| |
|
Sadlej-LPol-fl |
Footnotes

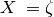 levels
available. Several intermediate levels of diffuse space between the customary
non-augmented and augmented versions have been supplied for each basis set,
including heavy-augmented and Truhlar’s [Papajak:2011:10] calendar
truncations described in Table Months Bases. Fitting bases
in Tables JKFIT,
RI, and DUAL
are available for methods incorporating density-fitting or dual-basis
approximations. JKFIT sets are appropriate for fitting
levels
available. Several intermediate levels of diffuse space between the customary
non-augmented and augmented versions have been supplied for each basis set,
including heavy-augmented and Truhlar’s [Papajak:2011:10] calendar
truncations described in Table Months Bases. Fitting bases
in Tables JKFIT,
RI, and DUAL
are available for methods incorporating density-fitting or dual-basis
approximations. JKFIT sets are appropriate for fitting 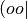 -type products,
such as encountered in SCF theory and the electrostatics/exchange terms of SAPT.
RI sets are appropriate for fitting
-type products,
such as encountered in SCF theory and the electrostatics/exchange terms of SAPT.
RI sets are appropriate for fitting 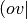 -type products, such as encountered in
MP2 and most SAPT terms. Citations for basis sets can be found in their
definition files at psi4/lib/basis in the source. For basis set availability by
element and the default value for keyword PUREAM, consult
Appendix Basis Sets by Element.
-type products, such as encountered in
MP2 and most SAPT terms. Citations for basis sets can be found in their
definition files at psi4/lib/basis in the source. For basis set availability by
element and the default value for keyword PUREAM, consult
Appendix Basis Sets by Element.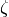
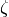
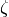
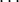 ,
, 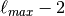 ,
, 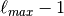 ,
, 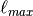
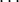 ,
, 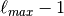
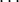 ,
, 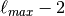 ,
, 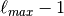 ,
, 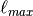
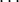 ,
, 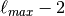 ,
, 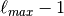
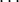 ,
, 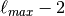
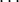
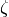 has
has 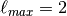 or d.
T
or d.
T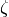 has
has 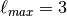 or f.
Q
or f.
Q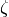 has
has 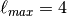 or g, etc.
or g, etc.